algorithm-suffix-tree

22. 后缀树suffix tree

简介

模式匹配是一个在工作中经常会用到的场景，比如说给定一个字符串数组txt[0..n-1]和要匹配的模式pat[0..m-1]，我们希望找出所有在txt中能够匹配模式字符串的次数。这就叫做模式匹配。

要想完成字符串匹配的任务，我们其实有两种方式，第一种方式就是使用各种模式匹配的算法，比如KMP，Rabin Karp，Finite Automata based和Boyer Moore。 这些匹配算法最好的时间复杂度是O(n)，其中n是字符串的长度 。

还有一种方式是对要查询的字符串数组进行预处理，处理过后再进行匹配的话，时间复杂度可以减少到O(m)，其中m是要匹配的模式的长度。

实际上这就是空间换时间的概念，假如我们有一本康熙字典，即使是O(n)的时间复杂度也住够长了，如果能够进行预处理之后，O(m)的时间复杂度将会大大减少我们的搜索时间。

那么是不是所有的字符串的模式匹配都可以使用预处理呢？

当然不是，因为预处理是需要耗费时间的，预处理的情况只适用于一次字符串数组很少发生变化，而相对的查询又比较多的情况。或者说一次预处理，多次查询的情况。

今天要介绍的后缀树就是预处理字符串数组的一种非常有效的方式。

字典树Trie

在介绍后缀树之前，我们先介绍一个字典树Trie。

上面是两个字典树的例子，我们来总结一下Trie树的特点：

1. Trie树中除了Root节点之外，其他的每个子节点都只包含一个字符。

2. 每个节点都可以有字母表个子节点，这些子节点不能重复。

3. 从根节点到每个叶子节点的字符连接起来是一个有效的字典中存储的字符串。

压缩字典树

我们看一下上面的字典树的特征，除了共享的节点之外，剩余的节点都创建成一个树就有点浪费了，我们可以尝试将剩余的节点都压缩到一个节点里面，我们看下示意图：

这样的树就叫做压缩字典树。

后缀树Suffix Tree

什么是后缀树呢？后缀树是一种压缩字典树，不同的是后缀树存储的是一个单词的所有后缀。

举个例子，如果我们要存储一个单词叫做BANANA，我们以标志$作为单词的结尾，那么BANANA有多少后缀呢？

0:banana$
1:anana$
2:nana$
3:ana$
4:na$
5:a$
6:$

将这些所有的后缀都使用上面的压缩字典树来表示的话，我们得到了下面的树：

后缀树的搜索

后缀树的搜索就是查找所有以要搜索的字符串开头的所有的单词。

比如我们要搜索na，那么匹配na的所有后缀有2和4两个节点。我们看下动画表示这个搜索过程：

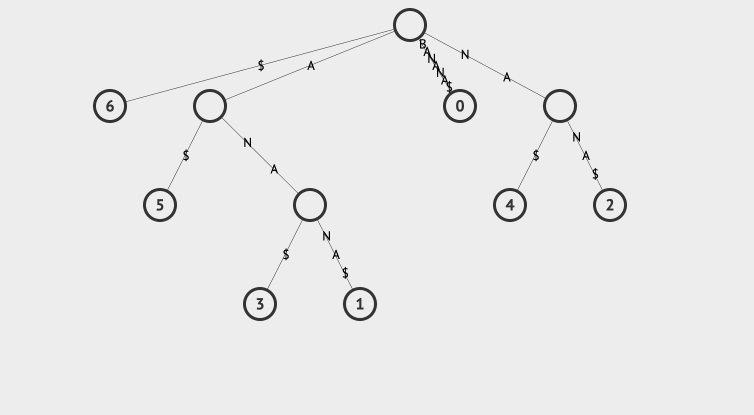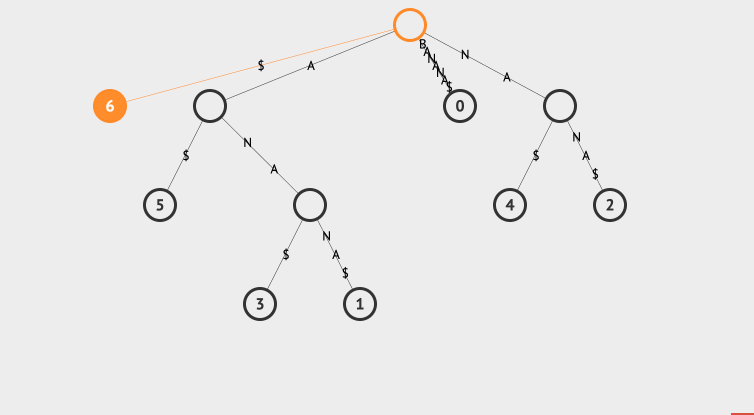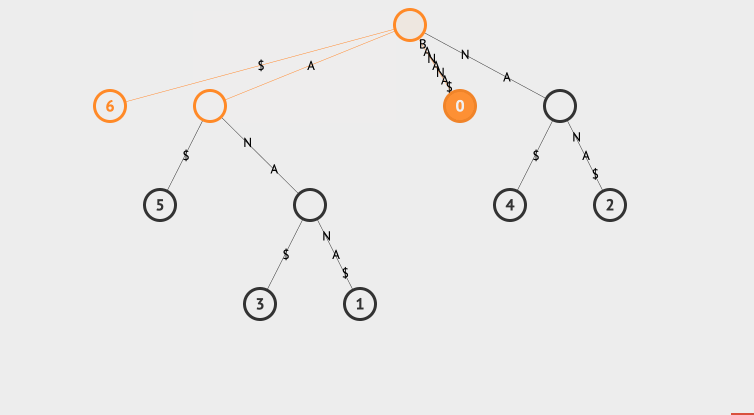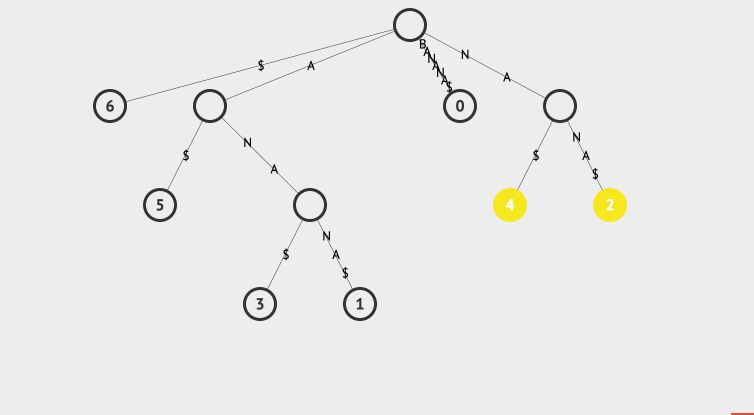
我们来解释一下这个搜索过程，首先从root开始，查看其子节点中有没有匹配na的，如果没有搜索就结束了。

如果有，则取出匹配na这条边的所有子节点。

查找最长重复子字符串

后缀树除了查找前缀匹配的字符之外，还有一个非常重要的作用就是查找最长重复子字符串。

怎么查找呢？ 因为后缀树中重复的字符串是作为共享的树的子节点来使用的。我们可以从根节点开始遍历，如果叶子节点是结束标志则直接跳过。

如果叶子节点不是结束标志，则递归遍历该叶子节点，找到其中的最长的重复字符串。这样遍历所有的字节点，将每个子节点中的最长的重复字符串进行对比，找到其中最长的那个。

我们看下查找最长重复子字符串的动画：

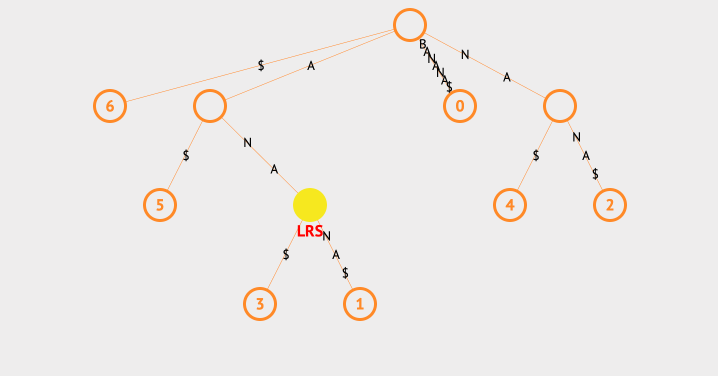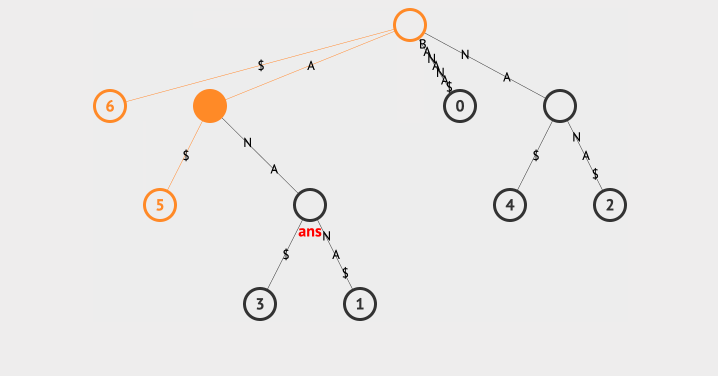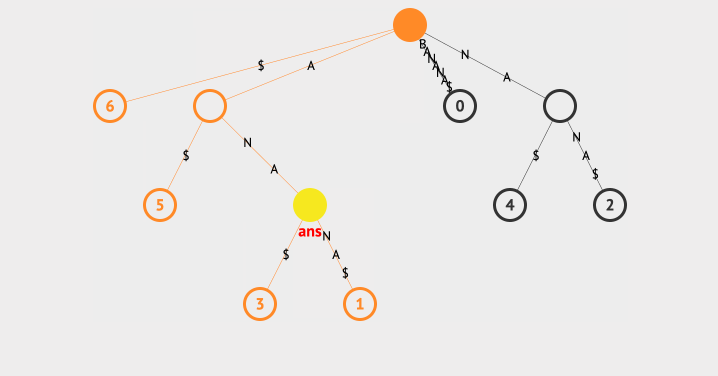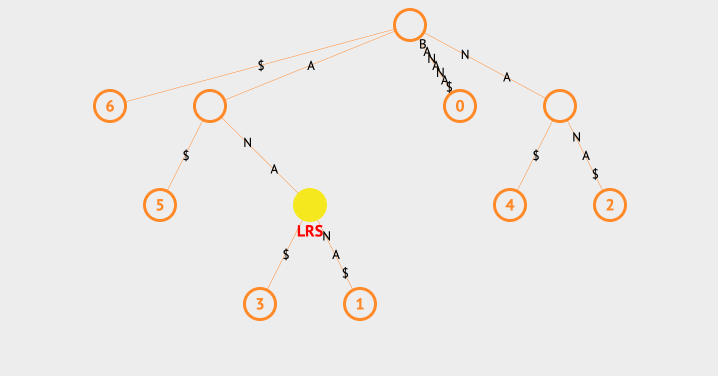
上面的例子中，我们使用一个ans来存放最长的字符串，每次找到子节点后，都会去判断该节点的共同字符串和ans的长度大小，以此来保存最长的那一个。

查找两个字符串的最长公共子字符串

上面的例子中我们是查询一个字符串中的重复字符串，如果想要查找两个两个字符串的最长公共子字符串该怎么做呢？

其实我们可以借鉴单个字符串的最长重复子字符串的例子。

不同的是，我们需要首先把两个字符串构建在同一个后缀树中，在构建的过程中，我们还需要对每个节点进行标记，以说明该节点是否两个字符串共有的，如果不是共有的，那么在查找的过程中就不需要继续到子节点去查找了。

然后借助于查找最长重复子字符串的流程就可以了，我们看下两个字符串BANANA和TANA的例子：

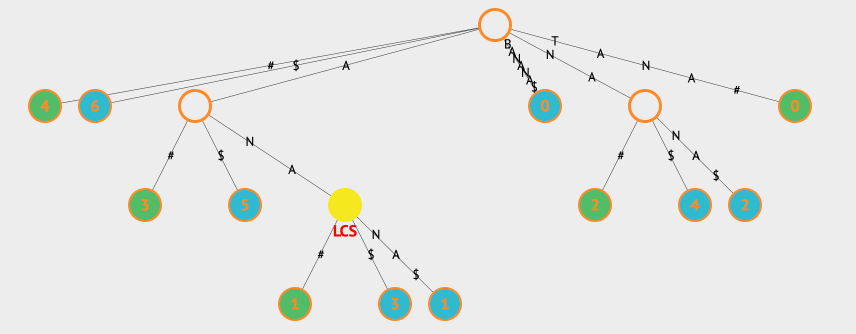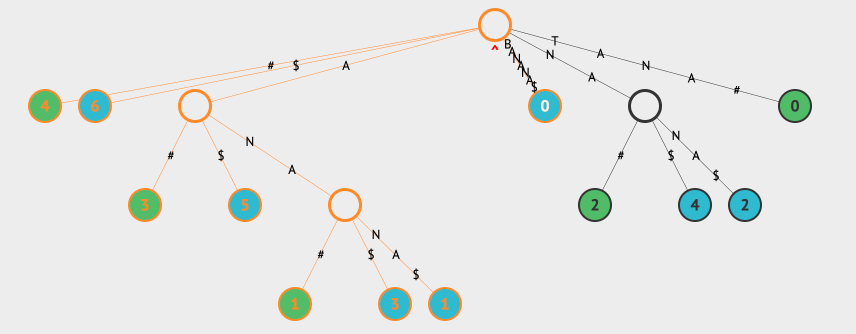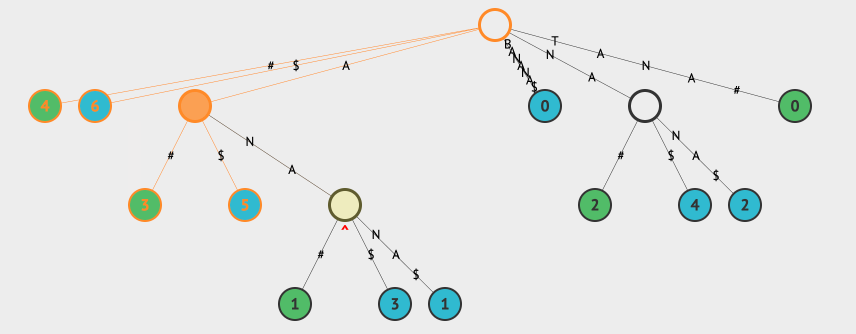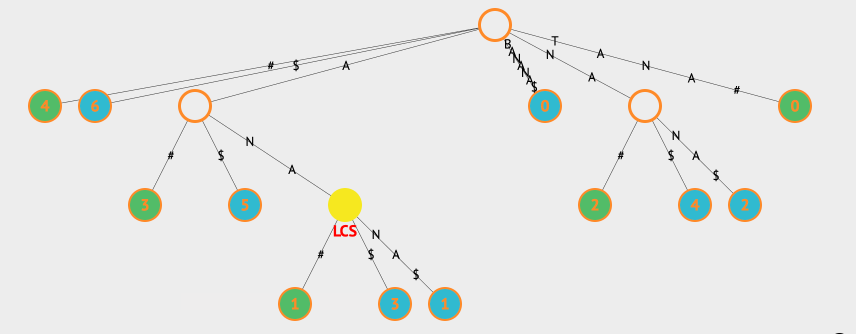
上面的例子中，LCS表示的是Longest Common Substring，我们同时用两种不同的颜色表示该节点属于哪一个字符串。

后缀树的代码实现

后缀树的代码实现有点复杂，这里我们直接在网上找到的一个实现。给大家简单讲解一下。

首先我们构建一个SuffixTrieNode，这个node中，我们保存一个indexes list，这里存储的是该节点在字符串中出现的位置。

并且还提供了插入和搜索的方法：

public class SuffixTrieNode {

    final static int MAX_CHAR = 256;

    SuffixTrieNode[] children = new SuffixTrieNode[MAX_CHAR];
    List<Integer> indexes;

    SuffixTrieNode() // Constructor
    {
        // Create an empty linked list for indexes of
        // suffixes starting from this node
        indexes = new LinkedList<Integer>();

        // Initialize all child pointers as NULL
        for (int i = 0; i < MAX_CHAR; i++)
            children[i] = null;
    }

    // A recursive function to insert a suffix of
    // the text in subtree rooted with this node
    void insertSuffix(String s, int index) {

        // Store index in linked list
        indexes.add(index);

        // If string has more characters
        if (s.length() > 0) {

            // Find the first character
            char cIndex = s.charAt(0);

            // If there is no edge for this character,
            // add a new edge
            if (children[cIndex] == null)
                children[cIndex] = new SuffixTrieNode();

            // Recur for next suffix
            children[cIndex].insertSuffix(s.substring(1),
                    index + 1);
        }
    }

    // A function to search a pattern in subtree rooted
    // with this node.The function returns pointer to a
    // linked list containing all indexes where pattern
    // is present. The returned indexes are indexes of
    // last characters of matched text.
    List<Integer> search(String s) {

        // If all characters of pattern have been
        // processed,
        if (s.length() == 0)
            return indexes;

        // if there is an edge from the current node of
        // suffix tree, follow the edge.
        if (children[s.charAt(0)] != null)
            return (children[s.charAt(0)]).search(s.substring(1));

            // If there is no edge, pattern doesnt exist in
            // text
        else
            return null;
    }
}

有了node，我们就可以使用了：

public class SuffixTree {

    SuffixTrieNode root = new SuffixTrieNode();

    // Constructor (Builds a trie of suffies of the
    // given text)
    SuffixTree(String txt) {

        // Consider all suffixes of given string and
        // insert them into the Suffix Trie using
        // recursive function insertSuffix() in
        // SuffixTrieNode class
        for (int i = 0; i < txt.length(); i++)
            root.insertSuffix(txt.substring(i), i);
    }

    /* Prints all occurrences of pat in the Suffix Trie S
    (built for text) */
    void searchTree(String pat) {

        // Let us call recursive search function for
        // root of Trie.
        // We get a list of all indexes (where pat is
        // present in text) in variable 'result'
        List<Integer> result = root.search(pat);

        // Check if the list of indexes is empty or not
        if (result == null)
            System.out.println("Pattern not found");
        else {

            int patLen = pat.length();

            for (Integer i : result)
                System.out.println("Pattern found at position " +
                        (i - patLen));
        }
    }

    // driver program to test above functions
    public static void main(String args[]) {

        // Let us build a suffix trie for text
        String txt = "www.flydean.com";
        SuffixTree S = new SuffixTree(txt);

        System.out.println("Search for 'ww'");
        S.searchTree("ww");

        System.out.println("\nSearch for 'flydean'");
        S.searchTree("flydean");

        System.out.println("\nSearch for 'ea'");
        S.searchTree("ea");

        System.out.println("\nSearch for 'com'");
        S.searchTree("com");
    }
}

本文已收录于 www.flydean.com

最通俗的解读，最深刻的干货，最简洁的教程，众多你不知道的小技巧等你来发现！

欢迎关注我的公众号:「程序那些事」,懂技术，更懂你！