> For the complete documentation index, see [llms.txt](https://docs.flydean.com/www.flydean.com/llms.txt). Markdown versions of documentation pages are available by appending `.md` to page URLs; this page is available as [Markdown](https://docs.flydean.com/www.flydean.com/docs/algorithm/01-anime/algorithm-cyclefinding.md).

# algorithm-cyclefinding

## 17. 环检测算法-弗洛伊德的兔子和乌龟

## 简介

环检测应该是一个非常常见的算法问题，怎么判断是否有环的问题呢？

一个很简单的做法就是用HashSet来保存要遍历的数据，如果出现了重复就知道这个链表是有环的。但是这个方法需要保存遍历过的所有的元素，所以其空间复杂度是o(n)。

有没有什么方法可以不用保存之前的元素也能够判断是否有环呢？

来看看弗洛伊德的兔子和乌龟算法吧。

## 弗洛伊德简介

有的同学会说了，弗洛伊德（Sigmund Freud）谁不知道，梦的解析的作者，大名鼎鼎的心理学专家，精神分析学派的创始人。

但是这里我们讲的弗洛伊德全名是Robert W．Floyd（罗伯特·弗洛伊德）而不是Sigmund Freud。

罗伯特·弗洛伊德是计算机科学家，图灵奖得主，前后断言法的创始人，堆排序算法和Floyd-Warshall算法的创始人之一。

它获得了1978年图灵奖，是一位“自学成才的计算机科学家”。

这个兔子和乌龟算法就是他发明的一种环检测算法。

## 构造一个环

在学习环状检测之前，我们先要够造一个环。程序是数学和计算机的优美结合。我们是不是可以考虑用数学的方法来构造一个环状结构呢？

假如我们用f(x)来表示这个函数，链表中的每一个元素都是调用f(x)的结果，并且我们将前一个节点的值作为下一个节点f(x)的输入，最后我们将会得到一个下面的集合：

{x0, x1 = f(x0), x2 = f(x1), ..., xi = f(xi-1), ...}

假设f(x)是一个一元二次方程，并且最后的结果对于特定的M取模，那么从x1 到 xi他们的取值范围肯定是在0-M之间。

一直重复下去，肯定会出现一个环形的结构。也就是说一定会出现 xi=xn。

这样我们的环状函数就出来了：

```java
    //环路生成函数
    //以这样的形式来生成数据：{x0, x1 = f(x0), x2 = f(x1), ..., xi = f(xi-1), ...}
    public static int f(int x){
        return (3*x*x+7*x+5)%97;
    }
```

假如我们的初始化输入是62，那么我们将会得到下面的一个环状结构：

![](https://img-blog.csdnimg.cn/20200818142256497.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_0,text_aHR0cDovL3d3dy5mbHlkZWFuLmNvbQ==,size_25,color_8F8F8F,t_70)

## 环的检测和入口定位

一般来说，我们需要找到环的入口点和环的长度。在弗洛伊德的兔子和乌龟算法中，我们假设乌龟和兔子同时出发，兔子的速度是乌龟的两倍。

也就是说对于初始位置为x0来说，乌龟的下一个位置是f(x0),而兔子的下一个位置是f(f(x0))。

因为兔子的速度是乌龟的两倍，如果链表出现环的情况下，兔子一定会追上乌龟。

这样我们通过判断兔子和乌龟的值是否相等，就可以判断整个链接是否有环。

我们来看一个直观的动画，其中蓝色的点表示的是乌龟，橙色的表示兔子：

![](https://img-blog.csdnimg.cn/20200818144141840.gif)

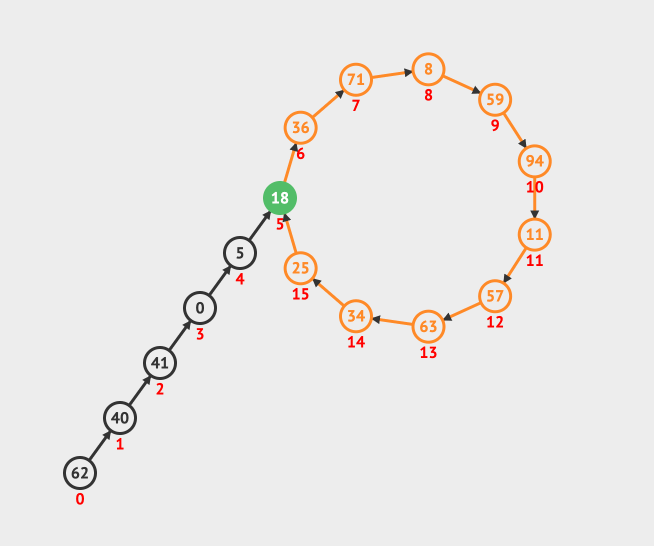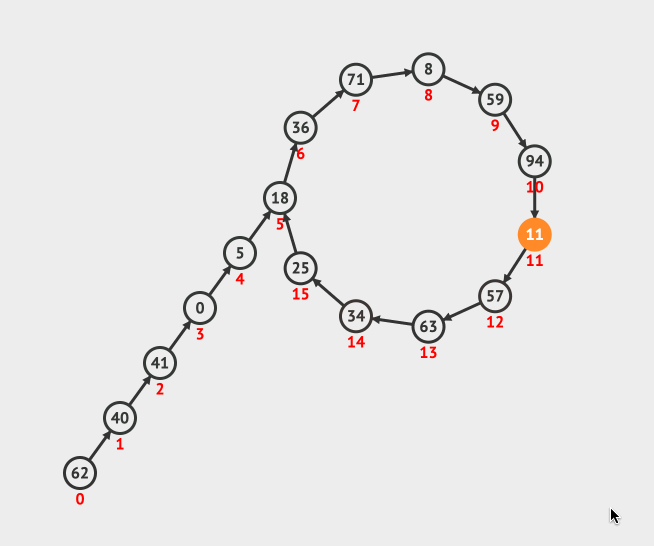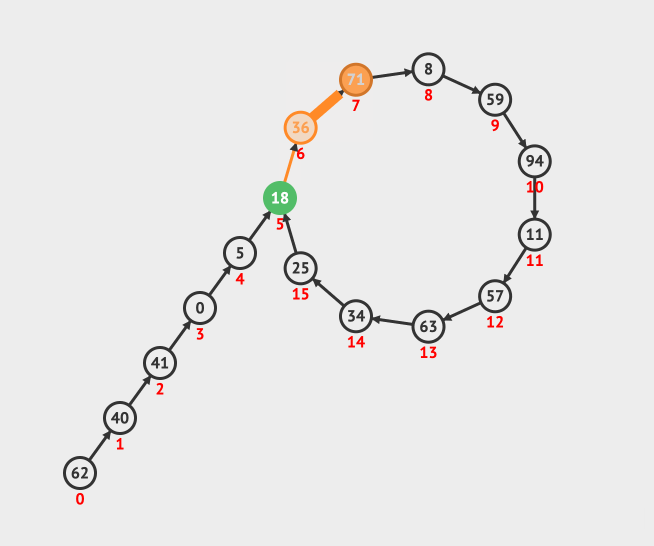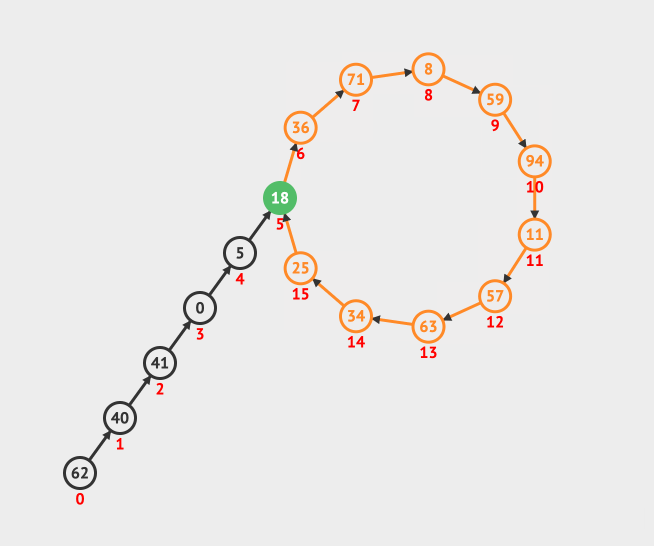
上面的动画做了三个事情：

1. 判断是否有环
2. 找到环的入口
3. 找到环的长度

对于的java代码如下：

```java
public class CycleFinding {

    public static int entryStep;
    public static int entryPoint;
    public static int cycleLongth;

    //环路生成函数
    //以这样的形式来生成数据：{x0, x1 = f(x0), x2 = f(x1), ..., xi = f(xi-1), ...}
    public static int f(int x){
        return (3*x*x+7*x+5)%97;
    }

    //弗洛伊德兔子乌龟-环检测算法
    public static void floydCycleFinding(int x){
        //第一步：让乌龟和兔子相遇
        // 我们定义两个值，一个是乌龟=f(x),一个是兔子，因为兔子的速度两倍于乌龟，所以我们可以用f(f(x))来表示兔子的值。
        int tortoise = f(x), hare = f(f(x));
        //然后乌龟和兔子一直向前走，直到他们的值相等，表明两者相遇了
        //注意，相遇点并不是环的入口点
        while (tortoise != hare) {
            tortoise = f(tortoise);
            hare = f(f(hare));
        }
        //第二步：找到环的入口点
        //让兔子重新从起点开始起跑，步长和乌龟一致，而乌龟继续原来的位置向后走，当两者相遇的点，就是环的入口点
        entryStep = 0; hare = x;
        while (tortoise != hare) {
            tortoise = f(tortoise);
            hare = f(hare); entryStep++;
        }
        entryPoint= tortoise;

        //第三步：找到环的步长
        //让兔子继续向前走，乌龟不动，当两者再次相遇的时候，就找到了步长
        cycleLongth = 1; hare = f(tortoise);
        while (tortoise != hare) {
            hare = f(hare); cycleLongth++;
        }
    }

    public static void main(String[] args) {
        floydCycleFinding(62);
        System.out.printf("entryPoint: %d,cycleLongth %d\n", entryPoint, cycleLongth);
    }
}
```

接下来我们分别一一来讨论

## 判断是否有环

判断是否有环很简单，我们只需要不断的比较兔子和乌龟的值即可：

```java
//第一步：让乌龟和兔子相遇
        // 我们定义两个值，一个是乌龟=f(x),一个是兔子，因为兔子的速度两倍于乌龟，所以我们可以用f(f(x))来表示兔子的值。
        int tortoise = f(x), hare = f(f(x));
        //然后乌龟和兔子一直向前走，直到他们的值相等，表明两者相遇了
        //注意，相遇点并不是环的入口点
        while (tortoise != hare) {
            tortoise = f(tortoise);
            hare = f(f(hare));
        }
```

## 找到环的入口

当乌龟和兔子相遇之后，怎么找到环的入口呢？

先来看一个相遇的示意图：

![](https://img-blog.csdnimg.cn/20200818105730311.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_0,text_aHR0cDovL3d3dy5mbHlkZWFuLmNvbQ==,size_25,color_8F8F8F,t_70)

假设在相应点的时候，乌龟行走的距离是x+y，那么对应的兔子行走的距离就是x+y+nL，其中L=y+z是环的长度。

因为兔子的速度是乌龟的两倍，所以我们可以得到下面的等式：

2(x+y)= x +y + nL

简化得到x+y = nL 。

将y 替换成为L-z，得到 x= （n-1）L + z 。

这个结论有么作用呢？

假如这个时候乌龟继续从相遇的节点出发，而兔子改成从初始节点出发，并且速度变成和乌龟一致。

那么当兔子走了x的距离的时候，乌龟刚好走了（n-1）L + z 的距离，也就是说兔子和乌龟将会在环的入口相遇。

我们的代码如下：

```java
        //第二步：找到环的入口点
        //让兔子重新从起点开始起跑，步长和乌龟一致，而乌龟继续原来的位置向后走，当两者相遇的点，就是环的入口点
        entryStep = 0; hare = x;
        while (tortoise != hare) {
            tortoise = f(tortoise);
            hare = f(hare); entryStep++;
        }
        entryPoint= tortoise;
```

## 找到环的长度

第三步是找到环的长度，这个很简单，我们让乌龟不动，兔子继续前行，等到再次相遇，走过的步数就是环的长度了。

```java
        //第三步：找到环的步长
        //让兔子继续向前走，乌龟不动，当两者再次相遇的时候，就找到了步长
        cycleLongth = 1; hare = f(tortoise);
        while (tortoise != hare) {
            hare = f(hare); cycleLongth++;
        }
```

本算法的空间复杂度是O(1)，而时间复杂度是O(n)。

本文的代码地址：

[learn-algorithm](https://github.com/ddean2009/learn-algorithm/tree/master/tree)

> 本文收录于 [www.flydean.com](http://www.flydean.com)
>
> 最通俗的解读，最深刻的干货，最简洁的教程，众多你不知道的小技巧等你来发现！
>
> 欢迎关注我的公众号:「程序那些事」,懂技术，更懂你！

![](https://img-blog.csdnimg.cn/20200709152618916.png)