algorithm-binary-heap

16. 二叉堆Binary Heap

简介

我们坐在高高的谷堆旁边，听妈妈讲那过去的事情。听到了堆，我就想起了这首歌。

没错，今天我们要介绍一个堆，这个堆叫做二叉堆。

二叉树我们之前讲过了，就是每个节点最多有两个子节点的树叫做二叉树。而二叉堆Binary Heap是一种特殊的二叉树。

二叉堆的特性

先看一个二叉堆的图，看看有什么特别的性质：

看起来二叉堆和二叉树没什么太大的区别。

但实际上还是有两点不一样。

1. 上面我们展示的是最大二叉堆，也就是说每个节点的值都要比它的任何子节点的值都要大。 同样的我们也可以构建最小二叉堆。

2. 第二个特性就是二叉堆是一个完全二叉树。

什么时候完全二叉树呢？

完全二叉树就是说二叉树的每一层都被填满了，除了最下面的一层，并且所有的最底层节点都尽力向左靠拢。

二叉堆的作用

二叉堆这样特殊的数据结构有什么作用呢？

因为二叉堆实际上是一个部分排序的序列，我们可以拿到二叉堆的堆顶元素，也就是最大的值，那么我们可以根据这个特性进行堆排序。

同时，二叉堆的这特性还可以用来实现优先队列，将优先级作为二叉堆的值，我们可以每次都拿到优先级最高的那个数据。

优先队 (PQ) 数据结构 和普通的队列差不多, 但是它多了以下两个主要操作:

1. enqueue(x): 放一个新元素 (键值) x 进去优先队

2. y =dequeue(): 返回已经在优先队里的有着最高优先级（键值）的元素 y。 如果存在优先级一样的情况，则先返回先入队的那个。也就是说像一个正常的Queue那样先进先出(FIFO)。

当然，还有其他的一些应用。

二叉堆的构建

二叉堆的底层实现可以用数组也可以用链表。这里我们使用数组来进行二叉堆的构建。

上图中的二叉堆，如果我们以层的存储顺序存放到数组中，那么应该是这样的：

arry[0] 一定是最大值。

同样的，我们可以得到下面的特性：

• array[(i-1)/2] i节点的父节点

• array[(2*i)+1] i节点的左子节点

• array[(2*i)+2] i节点的右子节点

我们可以得到下面的BinaryHeap的基本结构，这里我们添加了两个变量，一个是heapSize用来记录heap中存储的数据的个数，一个是capacity用来表示底层数组的最大容量。

public class BinaryHeap {

    //底层存储数组用来存储数据
    private int[] intArray;
    //heap大小
    private int heapSize;
    //数组容量
    private int capacity;

    //获取某个index的父节点
    private int parent(int i) { return (i-1)>>1; } // (i-1)/2
    //获取某个index的左子节点
    private int leftChild(int i) { return i<<1+1; } // i*2+1
    //获取某个index的右子节点
    private int rightChild(int i) { return (i<<1)+2; } // i*2+2

    public BinaryHeap(int capacity) {
        this.capacity= capacity;
        intArray = new int[capacity];
        intArray[0]=-1;
        heapSize = 0;
    }
}

获取二叉堆的最大值

获取二叉堆的最大值很简单，直接返回index=0的元素即可：

public int getMax() {
        return intArray[0];
    }

二叉堆的插入

先看一个二叉堆插入的动画：

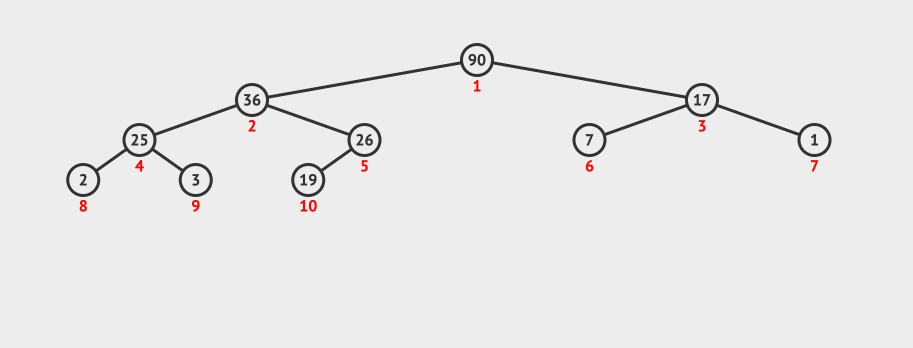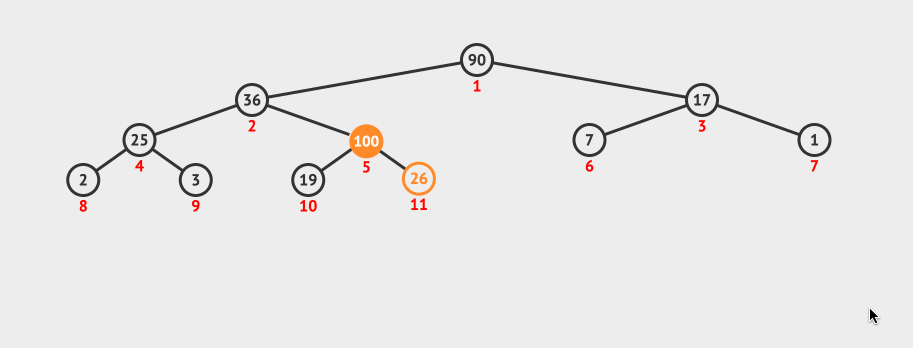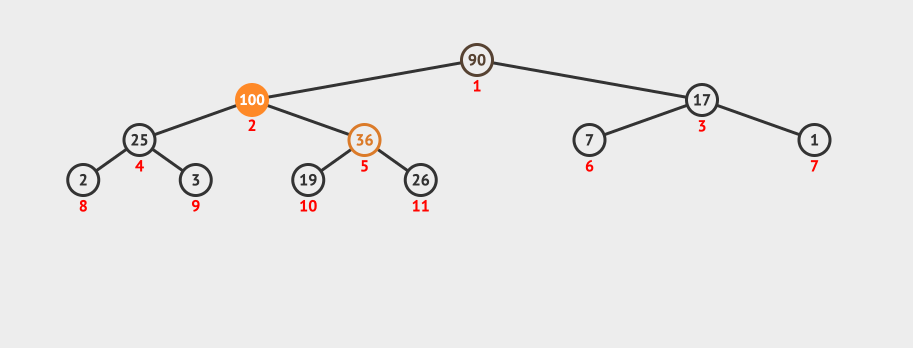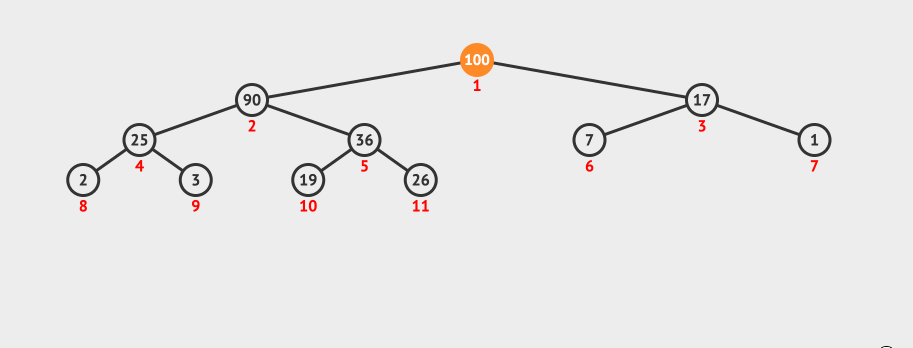
我们向现有的二叉堆中插入了一个100。

首先是插入到数组的最后一个元素，因为插入了新的元素100，而100大于它的父节点，所以需要对二叉堆进行节点调整。

这种调整我们叫做shiftUp，主要是将插入的节点和它的父节点做比较，如果大于父节点，则和父节点互换位置。然后再递归对父节点做shiftUp操作。

相对应的java代码如下：

//递归shift某个节点，将大值移动到最上面
    private void shiftUp(int i) {
        if (i == 0) return; // 如果是root，则不作操作
        if (intArray[i] > intArray[parent(i)]) { // 子节点大于父节点，则需要进行swap操作
            swap(intArray, i, parent(i)); // 将子节点和父节点进行互换
            shiftUp(parent(i)); // 递归shift父节点
        }
    }

有了shiftUp操作，我们可以总结一下insert操作的代码如下：

    //heap插入，插入到最后的位置，然后进行shift up操作
    public void insert(int x) {
        if(isFull()){
            expandHeap();
        }
        heapSize++;
        intArray[heapSize-1]= x; // 插入最后位置
        shiftUp(heapSize-1); // shift up

    }

insert操作的时间复杂度

insert直接向数组最后插入一个元素，然后遍历该元素的父节点，并一直到根节点。所以insert操作的时间复杂度应该是O(log N)。

二叉堆的提取Max操作

提取Max操作extractMax，就是从二叉堆中删除最大的元素。

先看一个删除最大元素的动画：

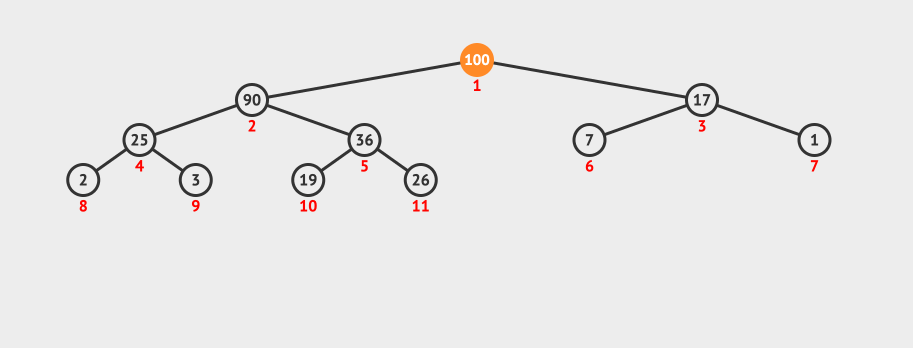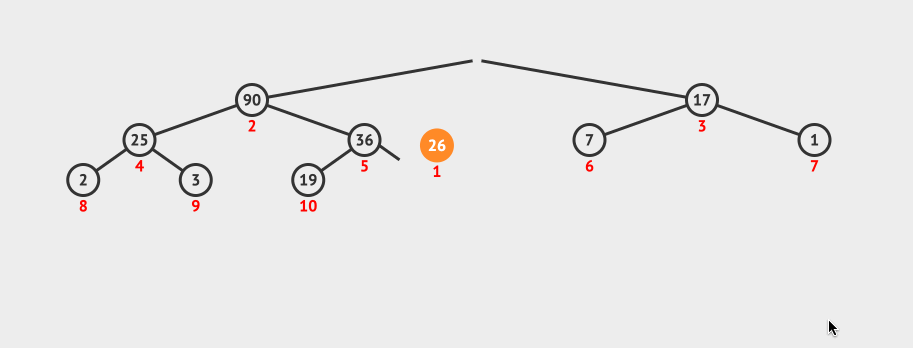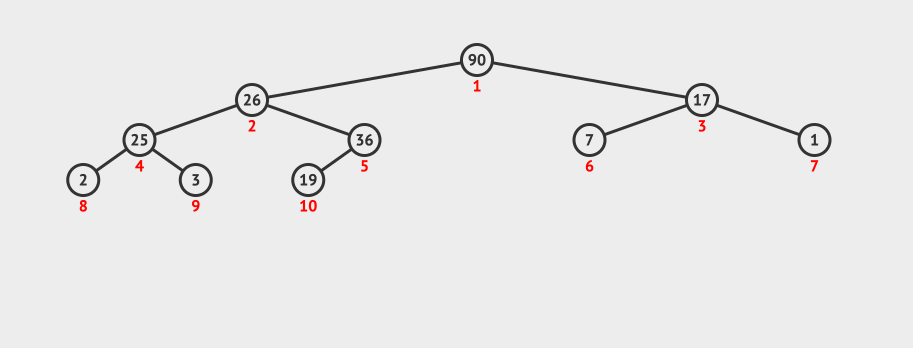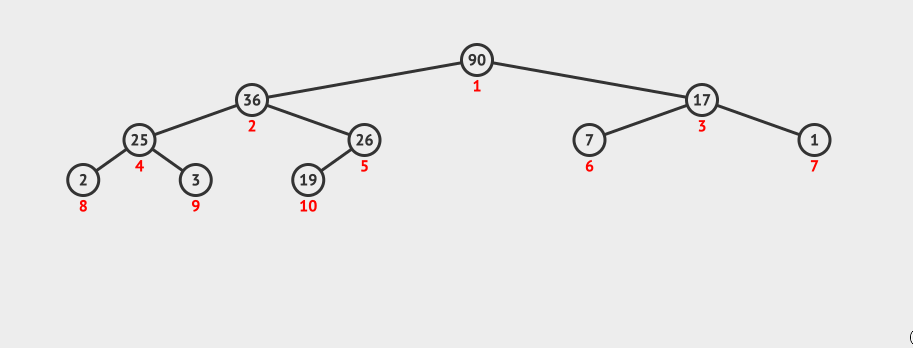
删除最大元素的流程是这样的，首先将100和数组中的最后一个元素互换位置，并将heapSize-1，表示已经删除了100这个元素。

现在数组中的26被放在index=0这个位置，但是26很明显不符合二叉堆的定义，所以需要将26元素下移，这个下移操作叫做shiftDown。

节点的左右子节点的大小是不确定的，如果我们想要找到子节点中最大的值，则需要进行两次比较。所以我们先进行左子节点的比较，再进行右子节点的比较，最后交互节点的数据，并继续递归shiftDown子节点。

对于的java代码如下：

//递归shift某个节点，将小值移动到最下面
    //比较过程是先比较左子节点，再比较右子节点
    private void shiftDown(int i) {
        if (i >= heapSize) return; // 超出了数组存储范围，直接返回
        int swapId = i; //要互换的id
        //如果存在左子节点，并且当前节点小于左子节点，则将要互换的id设置为左子节点
        if (leftChild(i) <= heapSize-1 && intArray[i] < intArray[leftChild(i)]){
            swapId = leftChild(i);
        }
        //如果存在右子节点，并且互换的id小于右子节点，则将互换的id设置为右子节点
        if (rightChild(i) <= heapSize-1 && intArray[swapId] < intArray[rightChild(i)]){
            swapId = rightChild(i);
        }
        if (swapId != i) { // 需要互换
            swap(intArray, i, swapId); // 进行互换
            shiftDown(swapId); // 递归要互换的节点
        }
    }

于是我们可以得到相应的ExtractMax()方法：

//获取最大的数据，
    public int extractMax() {
        int taken = intArray[0]; //root 就是最大的值
        swap(intArray, 0, heapSize-1); // 将root和最后一个值进行互换
        heapSize--;
        shiftDown(0); // 递归执行shift Down操作
        return taken; // 返回root的值
    }

extractMax的时间复杂度

同样的，extractMax虽然会多进行一次子节点的比较，但是只会递归log N次，所以extractMax() 的时间复杂度是 O(log N)。

创建二叉堆

有了插入方法，很明显我们可以通过一个个的插入数据，来构架一个二叉堆：

        BinaryHeap pq = new BinaryHeap(20);
        pq.insert(5);
        pq.insert(2);
        pq.insert(7);
        pq.insert(3);

看下这种插入的动画：

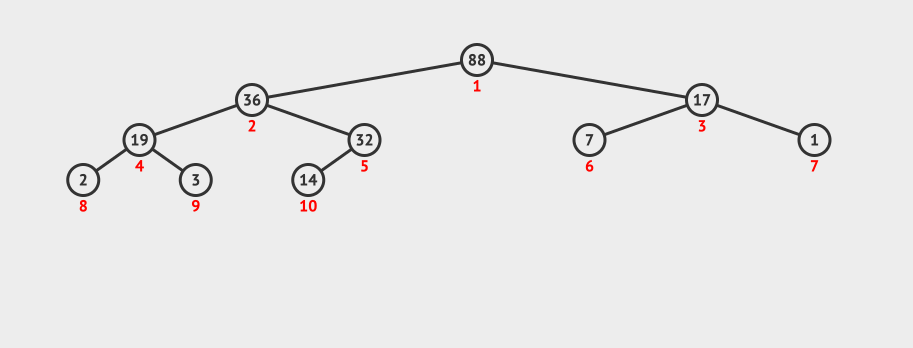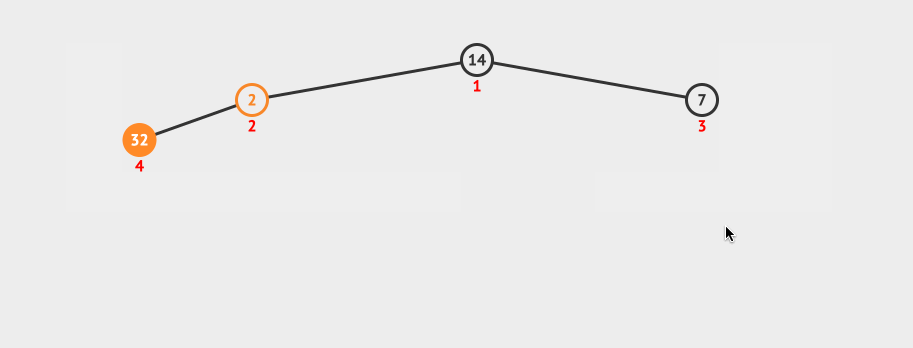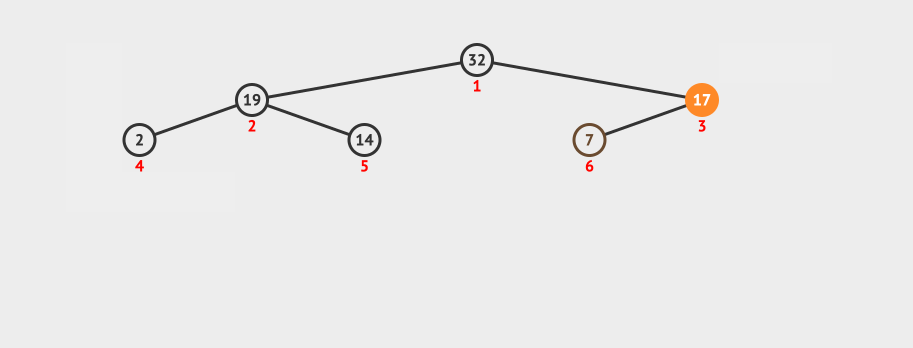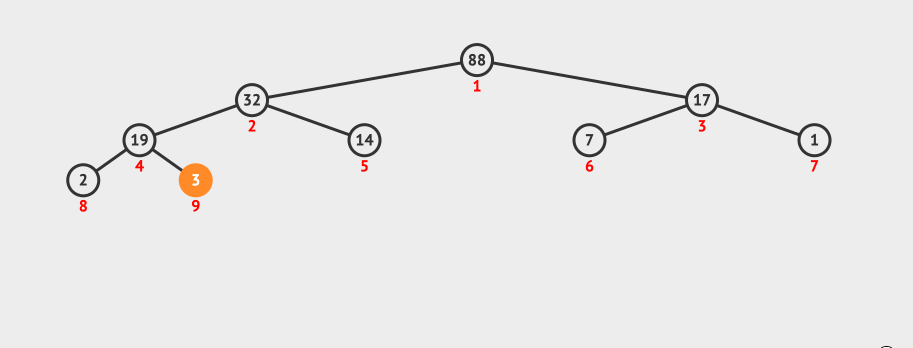
因为这种创建方法，需要插入N个数据，并且每插入一个数据都需要进行logN次比较，所以它的时间复杂度是O(N log N)。

下面我们来看一个更快的方法：

因为二叉堆是一个完全二叉树，假设树中的元素个数为N，那么其中一半的元素都是叶子节点。也就是说有N/2个叶子节点。

那么我们只需要对现有数组中所有的非叶子节点进行shitDown操作就可以完成排序了。

// 构建二叉堆
        for (int i = n / 2 - 1; i >= 0; i--)
            shiftDown(arr, n, i);

看下这种创建的动画：

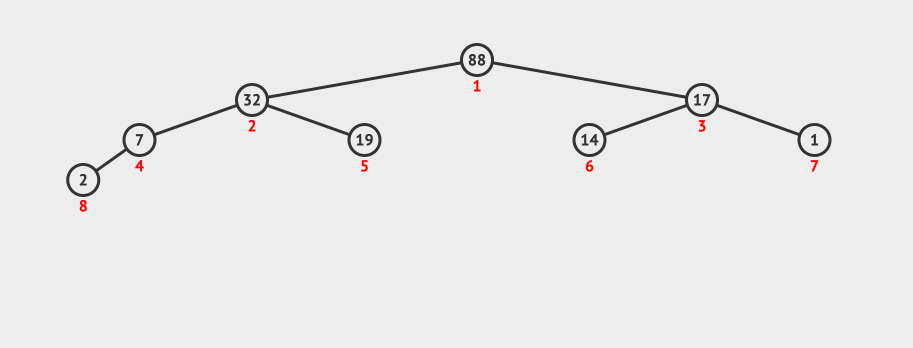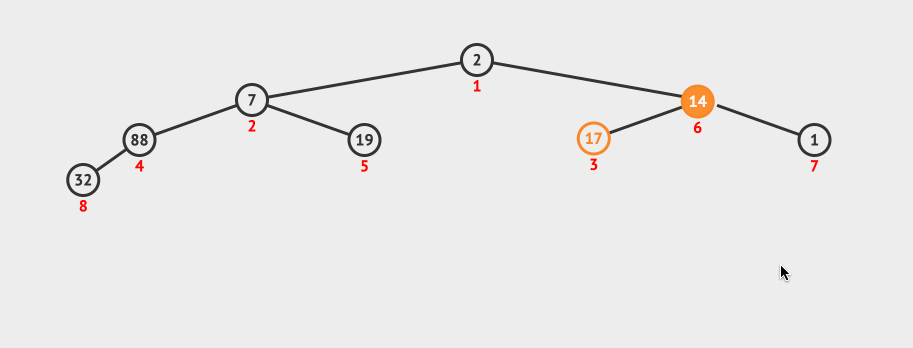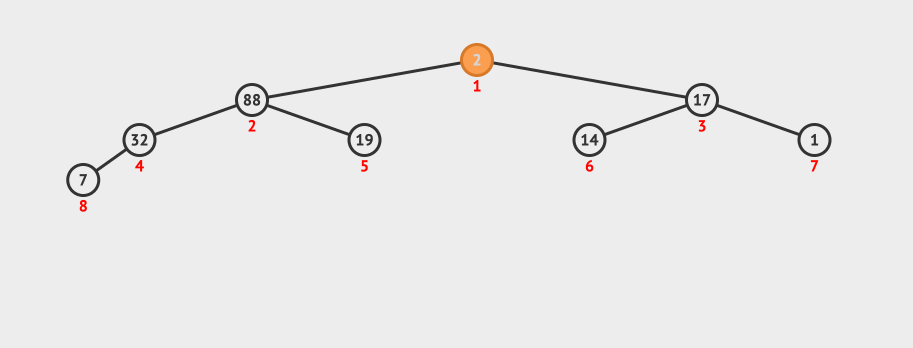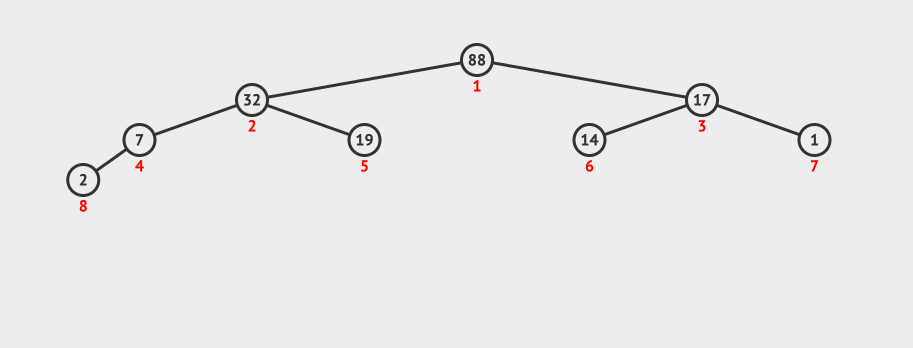
这种创建的时间复杂度是O(log N)。

本文的代码地址：

learn-algorithm

本文收录于 www.flydean.com

最通俗的解读，最深刻的干货，最简洁的教程，众多你不知道的小技巧等你来发现！

欢迎关注我的公众号:「程序那些事」,懂技术，更懂你！